Bij regressie kijken we naar de relatie tussen één of meerdere onafhankelijke variabelen (x) en de afhankelijke variabele (y). De meest simpele vorm van regressie is een rechte lijn, waarbij er sprake is van 1 x, en de vorm kan worden geschreven als y = a + bx.
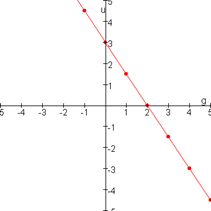
y : de afhankelijke variabele, of de uitkomst
b : helling (of stijging)
a : de intercept (daar waar de lijn de y-as kruist waar x = 0)
x : de onafhankelijke variable (de input)
Je kunt hiervoor gebruik maken van een tabel:
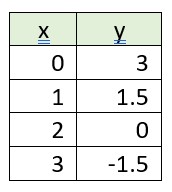
Voor elke toename van x + 1, neemt y met 1.5 af.
Daar waar x = 0 is y: 3, de intercept is hier 3; de helling is dan -1.5
Kijk nu naar de volgende tabel:
| # | ENGINESIZE | CYLINDERS | FUELCONSUMPTION_COMB | CO2EMISSIONS |
| 1 | 2 | 4 | 8.5 | 196 |
| 2 | 2.4 | 4 | 9.6 | 221 |
| 3 | 1.5 | 4 | 5.9 | 136 |
| 4 | 3.5 | 6 | 11.1 | 255 |
| 5 | 3.5 | 6 | 10.6 | 244 |
| 6 | 3.5 | 6 | 10 | 230 |
| 7 | 3.5 | 6 | 10.1 | 232 |
| 8 | 3.7 | 6 | 11.1 | 255 |
| 9 | 3.7 | 6 | 11.6 | ? |
De vraag is of we voor # 9 de uitstoot kunnen berekenen [y] aan de hand van de gegevens in de kolommen: EngineSize, Cylinders en FuelConsumption_Comb [x].
We maken hiervoor gebruik van multiple linear regression, met als gegeven input [x], en we zoeken de voorspelling van y, ŷ (uitgesproken als y-hat).
Laten we eerst kijken naar simple linear regression, waarbij gebruik gemaakt wordt van 1 input variabele, bijvoorbeeld de grootte van de motor. Als we dit plotten in een grafiek, zien we al snel dat de grootte van de motor samenhangt met de uitstoot.
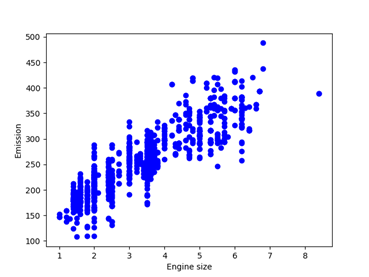
Als we nu meer variabelen toevoegen aan de berekening, dan wordt al snel zichtbaar dat ook hier verbanden bestaan:
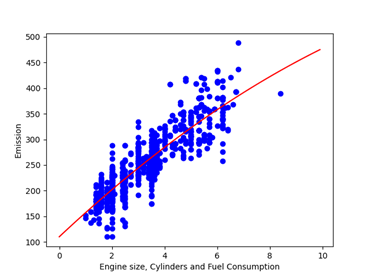
Hierdoor ziet de berekening er als volgt uit:
CO2EM = Ɵ0 + Ɵ1x1 + Ɵ2x2 + … + Ɵnxn
Of als vector:
Ŷ = ƟTx
Waarbij ƟT = [Ɵ0 , Ɵ1 , Ɵ2 , …] de parameters zijn en x de featureset (in dit geval de auto met zijn eigenschappen).
Download hier de dataset voor deze oefening.
De python code voor dit voorbeeld:
import matplotlib.pyplot as plt
import pandas as pd
import pylab as pl
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn import linear_model
#zorg er voor dat de data in de juiste directory staat
df = pd.read_csv(“FuelConsumptionCo2.csv”)
# bekijk de dataset
print(df.head())
# neem de gegevens die je kunt gebruiken als input (merk en model maakt hiervoor niet uit)
# en de verwachte output: CO2EMISSIONS
cdf = df[[‘ENGINESIZE’,’CYLINDERS’,’FUELCONSUMPTION_COMB’,’CO2EMISSIONS’]]
print(cdf.head(9))
# maak hiervan een diagram
plt.scatter(cdf.ENGINESIZE, cdf.CO2EMISSIONS, color=’blue’)
plt.xlabel(“Engine size”)
plt.ylabel(“Emission”)
plt.show()
msk = np.random.rand(len(df)) < 0.8
train = cdf[msk]
test = cdf[~msk]
train_x = np.asanyarray(train[[‘ENGINESIZE’]])
train_y = np.asanyarray(train[[‘CO2EMISSIONS’]])
test_x = np.asanyarray(test[[‘ENGINESIZE’]])
test_y = np.asanyarray(test[[‘CO2EMISSIONS’]])
poly = PolynomialFeatures(degree=2)
train_x_poly = poly.fit_transform(train_x)
train_x_poly
clf = linear_model.LinearRegression()
train_y_ = clf.fit(train_x_poly, train_y)
# De coefficienten
print (‘Coefficients: ‘, clf.coef_)
print (‘Intercept: ‘,clf.intercept_)
plt.scatter(train.ENGINESIZE, train.CO2EMISSIONS, color=’blue’)
XX = np.arange(0.0, 10.0, 0.1)
yy = clf.intercept_[0] + clf.coef_[0][1]*XX + clf.coef_[0][2]*np.power(XX, 2)
plt.plot(XX, yy, ‘-r’ )
plt.xlabel(“Engine size, Cylinders and Fuel Consumption”)
plt.ylabel(“Emission”)
plt.show()
from sklearn.metrics import r2_score
test_x_poly = poly.fit_transform(test_x)
test_y_ = clf.predict(test_x_poly)
print(“Mean absolute error: %.2f” % np.mean(np.absolute(test_y_ – test_y)))
print(“Residual sum of squares (MSE): %.2f” % np.mean((test_y_ – test_y) ** 2))
print(“R2-score: %.2f” % r2_score(test_y,test_y_ ) )
poly3 = PolynomialFeatures(degree=3)
train_x_poly3 = poly3.fit_transform(train_x)
clf3 = linear_model.LinearRegression()
train_y3_ = clf3.fit(train_x_poly3, train_y)
print (‘Coefficients: ‘, clf3.coef_)
print (‘Intercept: ‘,clf3.intercept_)
plt.scatter(train.ENGINESIZE, train.CO2EMISSIONS, color=’blue’)
XX = np.arange(0.0, 10.0, 0.1)
yy = clf3.intercept_[0]+ clf3.coef_[0][1]*XX + clf3.coef_[0][2]*np.power(XX, 2) + clf3.coef_[0][3]*np.power(XX, 3)
plt.plot(XX, yy, ‘-r’ )
plt.xlabel(“Engine size”)
plt.ylabel(“Emission”)
plt.show()
test_x_poly3 = poly3.fit_transform(test_x)
test_y3_ = clf3.predict(test_x_poly3)
print(“Mean absolute error: %.2f” % np.mean(np.absolute(test_y3_ – test_y)))
print(“Residual sum of squares (MSE): %.2f” % np.mean((test_y3_ – test_y) ** 2))
print(“R2-score: %.2f” % r2_score(test_y,test_y3_ ) )